الزوايا ومفردها الزاوية، هذا الكيان الهندسي البسيط الذي يتكون من تقاطع شعاعين في نقطة واحدة، يشكل حجر الأساس للعديد من المفاهيم الهندسية المعقدة. لطالما أثار هذا الشكل الهندسي اهتمام العلماء والباحثين، وذلك لما يحمله من خصائص هندسية فريدة وتطبيقات واسعة في مختلف المجالات. تتعدد أنواع الزوايا باختلاف قياسها وعلاقتها ببعضها البعض، ولكل نوع منها خصائص تميزه وتحدد تطبيقاته. في هذا المقال، سنتعرف على أهم أنواع الزوايا وخصائصها.
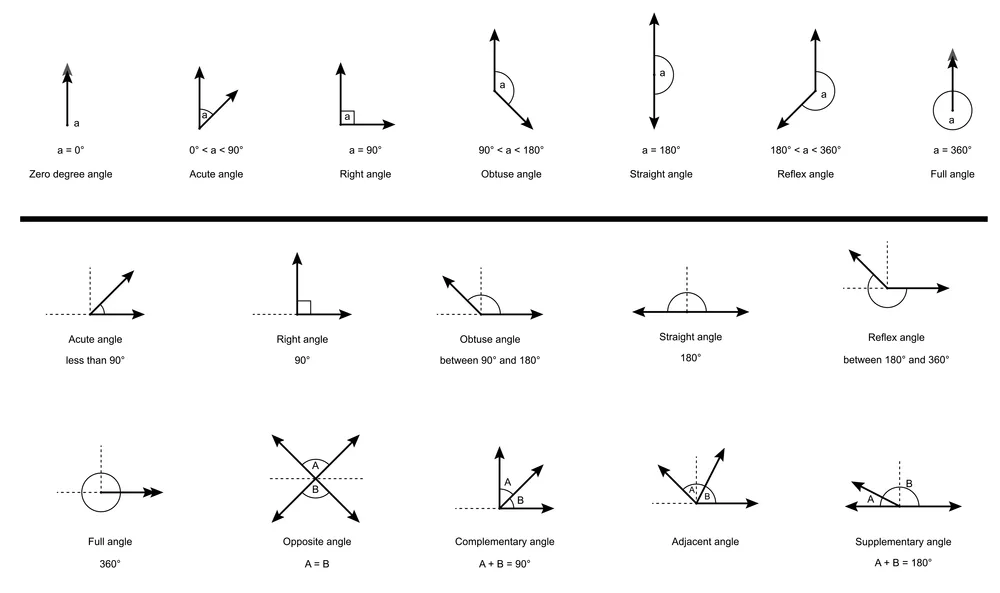
أنواع الزوايا تبعًا لقياسها:
تُصنف الزوايا حسب قياسها إلى عدة أنواع رئيسية، ولكل نوع خصائص هندسية تميزه عن غيره. إليك شرحًا مفصلاً لأنواع الزوايا المختلفة:
- الزاوية القائمة (Right Angle):
الزاوية القائمة هي أحد أهم الأنواع الأساسية للزوايا في الهندسة، ويتميز بقياسه الدقيق الذي يساوي 90 درجة. تتكون الزاوية القائمة من تقاطع شعاعين بشكل عمودي، بحيث يشكلان زاوية تساوي ربع دورة كاملة. يمكن تصور الزاوية القائمة على أنها الزاوية التي تتكون عند تقاطع ضلعي المربع أو المستطيل، وهي الزاوية التي تشكل أساسًا لبناء العديد من الأشكال الهندسية الأخرى. تتميز الزاوية القائمة بأهمية خاصة في الهندسة المعمارية والتصميم الصناعي، حيث تستخدم في بناء المباني والهياكل لضمان استقرارها وقوتها. كما تلعب الزاوية القائمة دورًا حاسمًا في العديد من التطبيقات الهندسية والفيزيائية.
- الزاوية الحادة (Acute Angle):
الزاوية الحادة هي أحد أنواع الزوايا الهندسية الأساسية، وتُعرف بأنها الزاوية التي قياسها أقل من 90 درجة. تخيل أنك تنظر إلى ركن حاد في غرفة، هذا هو مثال على الزاوية الحادة. وهي أصغر من الزاوية القائمة التي تشكل زاوية مستقيمة تمامًا مثل زاوية مربع. الزوايا الحادة موجودة في كل مكان حولنا، من زوايا المثلثات الحادة إلى زوايا الأشياء الحادة في الطبيعة. أهميتها تكمن في كونها اللبنة الأساسية للعديد من الأشكال الهندسية، وتستخدم في العديد من الحسابات الهندسية والفيزيائية.
- الزاوية المنفرجة (Obtuse Angle):
الزاوية المنفرجة هي تلك الزاوية التي تتجاوز قياسها 90 درجة ولكنها لا تصل إلى 180 درجة. تخيل أنك فتحت بابًا أكثر من الزاوية القائمة المعتادة، ولكن ليس إلى آخره، فالشكل الذي تشكله بين الباب والإطار هو مثال على زاوية منفرجة. هذه الزاوية أوسع وأكبر من الزاوية القائمة، ولكنها ليست مستقيمة تمامًا مثل الزاوية التي تشكلها عندما يكون الباب مفتوحًا على آخره. الزوايا المنفرجة موجودة في العديد من الأشكال الهندسية حولنا، مثل بعض أنواع المثلثات، وهي تلعب دورًا هامًا في العديد من الحسابات الهندسية.
- الزاوية المستقيمة (Straight Angle):
الزاوية المستقيمة هي زاوية قياسها 180 درجة، وتشكل خطًا مستقيمًا تمامًا. تخيل أنك قمت بطي ورقة إلى النصف، فالخط الناتج عن الطي يشكل زاوية مستقيمة. يمكننا تصور الزاوية المستقيمة على أنها نصف دورة كاملة. الزاوية المستقيمة لها أهمية كبيرة في الهندسة، فهي تستخدم في تعريف العديد من الأشكال الهندسية الأخرى مثل المستطيل والمربع، كما أنها أساس لحساب الزوايا الأخرى. علاوة على ذلك، عندما يكون مجموع قياس زاويتين 180 درجة، فإننا نقول إن هاتين الزاويتين متكاملتان، أي أنهما تشكلان معًا زاوية مستقيمة.
- الزاوية المحدبة أو المنعكسة (Reflex Angle):
الزاوية المحدبة أو المنعكسة هي نوع خاص من الزوايا يتميز بقياسه الكبير الذي يتجاوز قياس الزاوية المستقيمة (180 درجة) ولكنه أقل من قياس الدورة الكاملة (360 درجة). تخيل أنك تدور عقرب الساعة أكثر من نصف دورة كاملة، ولكنك لم تصل إلى نقطة البداية بعد، فإن الزاوية التي يشكلها عقرب الساعة مع موقعه الأصلي هي زاوية محدبة. هذه الزوايا لا تظهر بشكل شائع في الأشكال الهندسية البسيطة مثل المثلثات والمربعات، ولكنها توجد في العديد من التطبيقات الهندسية والفيزياء، مثل حساب الزوايا بين الكواكب أو في حركة الأجسام الدوارة.
- الزاوية الكاملة (Full Angle):
الزاوية الكاملة هي ببساطة دورة كاملة حول نقطة ما، وقياسها 360 درجة. تخيل أنك تدور حول نفسك حتى تعود إلى نفس الموضع الذي بدأت منه، فإن الزاوية التي تشكلها هذه الدورة هي زاوية كاملة. هذا النوع من الزوايا لا يشكل شكلاً هندسيًا محددًا مثل المثلث أو المربع، بل يمثل فكرة الدورة الكاملة أو الالتفاف الكامل حول نقطة ما. الزوايا الكاملة مهمة في العديد من المجالات، مثل الفيزياء حيث تستخدم لوصف الحركة الدورانية، والهندسة حيث تدخل في حسابات الزوايا الأخرى.
- الزاوية الصفرية (Zero angle):
الزاوية الصفرية هي حالة خاصة في الهندسة حيث يتطابق ضلعا الزاوية تمامًا، مما يؤدي إلى عدم وجود أي فتح بينهما. بعبارة أخرى، هي الزاوية التي قياسها صفر درجة. يمكن تخيلها كخط مستقيم واحد بدلاً من زاوية حقيقية. على الرغم من أنها قد تبدو غير بديهية للوهلة الأولى، إلا أن الزاوية الصفرية لها أهمية في بعض الحسابات الهندسية وفي بعض النماذج الرياضية. على سبيل المثال، في حساب الدورات الكاملة، يمكن اعتبار بداية ونهاية الدورة كزاويتين صفريتين.
أنواع الزوايا تبعًا لاتجاه قياسها
عند الحديث عن أنواع الزوايا تبعًا لاتجاه قياسها، فإننا نشير إلى الطريقة التي نقيس بها الزاوية وما إذا كنا نقيسها في اتجاه عقارب الساعة أو عكس اتجاه عقارب الساعة.
- الزوايا الموجبة (Positive Angles):
الزوايا الموجبة هي تلك التي نقيسها عكس اتجاه عقارب الساعة. تخيل أنك واقف في مركز دائرة وتنظر إلى نقطة محددة على محيطها. عندما تدور حول المركز عكس اتجاه عقارب الساعة لتصل إلى نقطة جديدة، فإن الزاوية التي تشكلتها هي زاوية موجبة. قياس هذه الزاوية يعبر عن مقدار الدوران الذي قمت به. تستخدم الزوايا الموجبة بشكل شائع في الرياضيات والفيزياء، خاصة في الحسابات المتعلقة بالحركة الدورانية، حيث تمثل الزاوية الموجبة زيادة في الزاوية الأصلية. بمعنى آخر، الزاوية الموجبة هي الزاوية التي تزداد قيمتها كلما دارنا عكس اتجاه عقارب الساعة.
- الزوايا السالبة (Negative Angles):
الزوايا السالبة هي تلك الزوايا التي تقاس في اتجاه عقارب الساعة، على عكس الزوايا الموجبة التي تقاس عكس اتجاه عقارب الساعة. تخيل أنك تقف في مركز دائرة، والزاوية الموجبة هي دورانك عكس اتجاه عقارب الساعة، بينما الزاوية السالبة هي دورانك في اتجاه عقارب الساعة.
تستخدم الزوايا السالبة بشكل شائع في الرياضيات والفيزياء، خاصة في الحسابات المتعلقة بالحركة الدورانية. على سبيل المثال، في الدوائر المثلثية، يمكن تمثيل الزوايا السالبة كدوران عكس اتجاه الزوايا الموجبة. كما تستخدم الزوايا السالبة في وصف الحركات الدورانية في الاتجاه المعاكس للحركة الموجبة.
مثال توضيحي للزاويتين: إذا قمت بقياس زاوية مقدارها 30 درجة عكس اتجاه عقارب الساعة، فإننا نحصل على زاوية موجبة قياسها 30 درجة. ولكن إذا قمنا بقياس نفس الزاوية ولكن في اتجاه عقارب الساعة، فإننا نحصل على زاوية سالبة قياسها -30 درجة.
أنواع الزوايا تبعًا لعلاقاتها مع بعضها البعض
بالإضافة إلى تصنيف الزوايا حسب قياسها واتجاه قياسها، يمكن أيضًا تصنيفها بناءً على العلاقة التي تربط بين زاويتين أو أكثر. إليك بعض أهم هذه العلاقات:
- الزوايا المتكاملة (Supplementary Angles):
الزوايتان المتكاملتان هما زاويتان مجموعهما 180 درجة. تخيل خطًا مستقيمًا، الزاويتان المتكاملتان هما الزاويتان اللتان تشكلان هذا الخط المستقيم عندما تلتقيان عند نقطة واحدة. بمعنى آخر، إذا وضعت زاويتين متكاملتين جنبًا إلى جنب بحيث يتطابق ضلع من كل زاوية، فإن الضلعان الآخران سيستقيمان معًا لتشكيل خط مستقيم. إذا كانت زاوية قياسها 70 درجة، فإن الزاوية المتكاملة لها قياس 180 – 70 = 110 درجة.
تعتبر الزوايا المتكاملة مهمة جدًا في الهندسة، فهي تساعدنا في حساب قياسات الزوايا المجهولة، وفي فهم العلاقات بين الأشكال الهندسية المختلفة. على سبيل المثال، الزاويتان المتجاورتان على خط مستقيم هما دائمًا زاويتان متكاملتان.
- الزوايا المتتامة (Complementary Angles):
الزوايا المتتامة هي زوج من الزوايا التي يكون مجموع قياسيهما 90 درجة، أي ربع دائرة. بعبارة أخرى، عندما تجمع قياس زاويتين متتامتين، فإن النتيجة هي زاوية قائمة. تخيل أن لديك زاوية حادة، الزاوية التي تكملها لتصل إلى 90 درجة هي الزاوية المتتامة لها. لا يشترط أن تكون الزاويتان المتتامتان متجاورتين، أي لا يشترط أن يكون لهما ضلع مشترك، فما يهم هو أن مجموع قياسيهما يساوي 90 درجة.
مثال: إذا كانت لدينا زاوية قياسها 30 درجة، فإن الزاوية المتتامة لها هي زاوية قياسها 60 درجة، لأن 30 درجة + 60 درجة = 90 درجة.
- الزوايا المتقابلة بالرأس (Vertical Angles):
الزوايا المتقابلة بالرأس هي تلك الزوايا التي تتكون عند تقاطع مستقيمين، حيث تتشارك هذه الزوايا في نفس الرأس ونفس الضلعين ولكن تكون متقابلة في الاتجاه. الميزة المميزة للزوايا المتقابلة بالرأس هي أنها متساوية في القياس دائماً. تخيل أنك ترسم خطين مستقيمين يتقاطعان، ستلاحظ أن الزاويتين اللتين تتكونان عند نقطة التقاطع وتكونان متقابلتين بالاتجاه ستكونان متساويتين في الحجم. تُستخدم هذه الخاصية بشكل واسع في حل المسائل الهندسية، حيث يمكننا إيجاد قياس زاوية مجهولة إذا عرفنا قياس الزاوية المتقابلة معها.
إذا كان لدينا خطان مستقيمان يتقاطعان، وتكون إحدى الزوايا المتقابلة بالرأس قياسها 60 درجة، فإن الزاوية المتقابلة الأخرى ستكون أيضًا قياسها 60 درجة.
- الزوايا المتجاورة (Adjacent Angles):
الزوايا المتجاورة هي تلك الزوايا التي تشترك في رأس واحد وضلع واحد على الأقل، بمعنى آخر هما زاويتان تقعان جنبًا إلى جنب وتتقاسمان أحد الأضلاع. يمكن تصور الزوايا المتجاورة كقطع من فطيرة متجاورة، حيث تشترك كل قطعتين في جزء من الحافة.
تختلف الزوايا المتجاورة عن بعضها البعض في قياسها، فقد تكون متساوية أو مختلفة. كما أنها قد تكون متكاملة (مجموع قياسهما 180 درجة) أو متتامة (مجموع قياسهما 90 درجة) أو لا تكون كذلك.
- الزاويتان المتناظرتان (Corresponding Angles):
الزاويتان المتناظرتان هما زاويتان تتشكلان عندما يقطع مستقيم مستقيمين متوازيين. تخيل أن لديك قطعتين من السكك الحديدية المتوازية، وعبرهما طريق. الزاويتان المتناظرتان هما الزاويتان اللتان تقعان في نفس الموضع بالنسبة للخطين المتوازيين والقاطع.
ببساطة، الزاويتان المتناظرتان هما مثل صورتين طبق الأصل لبعضهما البعض في أماكن مختلفة.
الخصائص الأساسية للزوايتين المتناظرتين:
- المساواة في القياس: أهم خاصية للزاويتين المتناظرتين هي أنهما متساويتان في القياس. أي أن إذا كانت إحدى الزاويتين المتناظرتين قياسها 60 درجة، فإن الزاوية الأخرى المتناظرة لها قياس 60 درجة أيضًا.
- الموقع: تقع الزاويتان المتناظرتان في نفس الموضع بالنسبة للخطين المتوازيين والقاطع.
- الأهمية: تستخدم الزوايا المتناظرة بشكل كبير في الهندسة لإثبات العديد من النظريات وحل المسائل الهندسية، خاصة تلك المتعلقة بالخطوط المتوازية والشكل الرباعي.
- الزاويتان المتبادلتان (Alternate Angles):
الزوايتان المتبادلتان هما زاويتان تتكونان عندما يقطع مستقيم مستقيمين متوازيين. تتميز هاتان الزاويتان بأنهما تقعان على جانبين متقابلين من القاطع (المستقيم الذي يقطع المستقيمين المتوازيين) وبين المستقيمين المتوازيين أنفسهم.
الخاصية الأساسية للزوايتين المتبادلتين هي أنهما متساويتان في القياس. هذه الخاصية هي حجر الزاوية في العديد من البراهين الهندسية وتستخدم بشكل متكرر في حل المسائل الهندسية المتعلقة بالتوازي. ببساطة، الزوايتان المتبادلتان هما زاويتان متساويتان تقعان في مواقع متقابلة بالنسبة لخطين متوازيين وخط قاطع لهما.
مثال: تخيل خطين للسكك الحديدية متوازيين وخطًا آخر يعبرهما (مثل طريق). الزوايا التي تتكون بين الخطوط الحديدية والطريق في الأماكن المتقابلة هي زوايا متبادلة ومتساوية في القياس.
وحدات قياس الزوايا
تستخدم وحدات قياس مختلفة لقياس الزوايا، ولكل وحدة منها استخداماتها الخاصة في مجالات مختلفة. إليك أهم هذه الوحدات:
- الدرجة (Degree):
الدرجة هي الوحدة الأكثر شيوعًا لقياس الزوايا، وهي تقسم الدائرة الكاملة إلى 360 جزءًا متساوياً ويُرمز لها بالرمز (°). بمعنى آخر، إذا قمنا بتقسيم دائرة إلى 360 جزءًا متساويًا، فإن كل جزء منها يمثل درجة واحدة. تعتبر الدرجة وحدة قياس سهلة الفهم والاستخدام في الحياة اليومية وفي الهندسة الأساسية، حيث تستخدم لقياس الزوايا في الأشكال الهندسية المختلفة، مثل المثلثات والمربعات والدوائر. كما تستخدم الدرجة في تحديد المواقع الجغرافية على الخرائط، حيث يتم تحديد خطوط الطول والعرض بالدرجات. بالإضافة إلى ذلك، تستخدم الدرجة في مجالات أخرى مثل الفلك والهندسة المعمارية والتصميم الصناعي.
- الراديان (Radian):
الراديان هو وحدة قياس الزوايا في الرياضيات والفيزياء، ويعتبر الوحدة القياسية المعتمدة في النظام الدولي للوحدات. على عكس الدرجة التي تقسم الدائرة إلى 360 جزءًا متساوياً، فإن الراديان يرتبط بطول القوس المقابل للزاوية في دائرة ذات نصف قطر واحد. بمعنى آخر، الراديان الواحد هو قياس الزاوية المركزية التي يقطع قوسها على محيط الدائرة طولًا مساويًا لنصف قطر الدائرة. هذه العلاقة الطبيعية بين الزاوية وطول القوس تجعل الراديان وحدة قياس أكثر ملاءمة في العديد من الحسابات الرياضية والفيزيائية، خاصة تلك المتعلقة بالحركة الدورانية.
- الرمز: يرمز للراديان بالحرف “rad” (عادةً لا يكتب).
- العلاقة بالدرجة: 2π راديان تساوي 360 درجة، أي أن 1 راديان يساوي تقريبًا 57.3 درجة.
- الغراد (Grad):
الغراد هي وحدة قياس للزوايا، أقل شهرة من الدرجة والراديان، ولكنها تستخدم في بعض الأحيان، خاصة في بعض الأنظمة القديمة أو المتخصصة. تقسم الدائرة الكاملة في نظام الغراد إلى 400 جزء متساوي، بمعنى أن كل غراد يعادل 1/400 من الدائرة الكاملة. هذه القيمة تجعل من السهل التعامل مع الزوايا القائمة، حيث أن الزاوية القائمة تساوي 100 غراد. وبالتالي، فإن الغراد يقدم نظامًا عشريًا لقياس الزوايا، مما يجعله أسهل في الحسابات في بعض الحالات. ومع ذلك، بسبب هيمنتي الدرجة والراديان في معظم المجالات العلمية والهندسية، فإن استخدام الغراد أصبح محدودًا نسبيًا.
- الدقيقة القوسية (Arc minutes):
الدقيقة القوسية هي وحدة قياس صغيرة جدًا للزوايا، وتستخدم عادة في المجالات التي تتطلب دقة عالية في القياس مثل الفلك والمساحة. هي عبارة عن جزء واحد من الستين من الدرجة، أي أن الدرجة الواحدة تساوي 60 دقيقة قوسية (‘)، والدقيقة تقسم إلى 60 ثانية قوسية (“). تستخدم الدقيقة القوسية لقياس الزوايا الصغيرة جدًا التي يصعب قياسها بالدرجات بشكل مباشر.
تستخدم الدقيقة القوسية في العديد من التطبيقات العملية، مثل تحديد المواقع بدقة على سطح الأرض، وقياس أبعاد الأجرام السماوية، وحساب المسافات بين النجوم والكواكب. كما تستخدم في علم الفلك لتحديد حركة الأجرام السماوية ودراسة الظواهر الفلكية بدقة عالية.
اكتشاف المزيد من عالم المعلومات
اشترك للحصول على أحدث التدوينات المرسلة إلى بريدك الإلكتروني.