تعريف المصفوفة

المصفوفة كمصطلحٍ استُعملت في ميادينَ عديدةٍ بتباينِ الزمانِ والموضعِ، ففي روما العتيقةِ كانتِ المصفوفةُ حيوانًا يُحفظُ للتربيةِ، أو يُطلقُ هذا المصطلحُ على النبتةِ الأصلِ التي تُستخدمُ بذورُها لإنتاجِ أصنافٍ أخرى من النباتاتِ.

وأمّا في اللغةِ الإنكليزيةِ كان لهذه الكلمةِ معانٍ كثيرةٌ؛ فعلماءُ الرياضياتِ استعملوها لتنظيمِ مُستطيلٍ من الأعدادِ أو الرموزِ التي تُستعملُ لإجراءِ حساباتٍ مُتباينةٍ، أمّا علماءُ الجيولوجيا استعملوها للدلالةِ على التربةِ أو الصخورِ التي يتمُ اكتشافُ مُستحثاتٍ فيها، وبصورةٍ عامةٍ كانتِ المصفوفةُ اختيارًا حسنًا كاسمٍ للواقعِ الذي يجدُ فيه جميعُ البشرِ أنفسَهم يعيشون في سلسلةٍ من أفلامِ الخيالِ العلميِّ المشهورةِ.

أُنشئ مُصطلح المصفوفة في عام 1848 على يد جي جي سيلفستر ليُطلق على تجميعةٍ مُرتّبةٍ من الأرقام. وفي سنة 1855، أوضح آرثر كايلي المصفوفة كتمثيلٍ لعناصرٍ ذات علاقةٍ خطيةٍ، وتُعتبر هذه الحقبة بدايةً لعلم الجبر الخطي ودراسة المصفوفات.

تعريف المصفوفة

تُعرّف بأنها تشكيلة من الأعداد مُنظّمة في هيئة صفوف وأعمدة، في الغالب تكون هذه الأعداد أعدادًا حقيقية، ومن الجائز أن تكون أعدادًا عقدية. بصورة عامة، تُعرّف أيضًا بأنها اقتران رياضي خطي يُحوّل نطاقًا (مجموعة المصدر) إلى مدى (مجموعة الهدف أو المُستقر).

قد تتألف كل من مجموعة البداية والنهاية من أعداد صحيحة أو مركّبة أو متجهات عددية، كما يجوز أن تتشكل هاتان المجموعتان من توابع رياضية أو متجهات توابع رياضية. يُعبّر عن المصفوفة بواسطة معقوفتين كبيرتين أو قوسين دائريين تُدوّن داخلهما مُدخلات المصفوفة كما هو مُبيّن في الشكل:

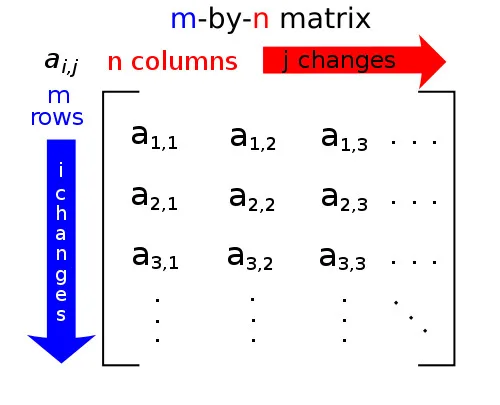
حيث a_ij أعداد صحيحة أو مركبة أو عقدية.

يُرمز للمصفوفة بحرفٍ لاتينيٍّ كبيرٍ وتحته عددين طبيعيين على شكل جداء هما m  و n  حيث m  عدد أسطر المصفوفة  و n عدد الأعمدة (مثال A_m*n ).

تُدعى الخطوط الأفقية في المَصفوفة بالأسطر بينما تُدعى الخطوط العمودية بالأعمدة، أما الأعداد تُدعى مدخلات المصفوفة أو عناصرها حيث لكل عنصرٍ موقع محدد.

يدل عادةً على أي مدخلٍ في المَصفوفة بحرفٍ لاتينيٍّ صغيرٍ وأسفله رقمين صغيرين بحيث يُمثل العدد الأول رقم الصف والثاني رقم العمود ( مثلاً: العنصر في الزاوية العليا اليسرى هو عنصر من العمود الأول والصف الأول وهكذا …).

تعاريف خاصة بالمصفوفات

• حيّز المصفوفة أو رتبتها أو قياسها: يعرّف بأنه عدد الأسطر في جداء عدد الأعمدة؛ أي إذا كان لدينا مصفوفة تحتوي على 5 أسطر و 3 أعمدة فإن قياسها أو رتبتها هو 3*5 .
• المتّجه: هو المصفوفة المؤلفة من صفٍ واحدٍ وعمودٍ واحدٍ، حيث أن المصفوفة ذات العمود الواحد يُرمز لها بالشكل A_m*1 وتعرف باسم متجه عمودي، بينما المصفوفة المؤلفة من صف واحد يُرمز لها ب A_1*n  وتعرف باسم متجه صفي.
• المصفوفة المربعة: هي مصفوفةٌ تحوي نفس العدد من الأسطر والأعمدة ويُرمز لها A_n*n كما في الشكل:
• المَصفوفة المنفردة: هي المصفوفة المربعة التي ليس لها نظيرٌ ضربيٌّ أما التي لها نظير ضربي تسمى غير منفردةٍ.
• المَصفوفة اللانهائية: هي المصفوفة التي تحوي على عددٍ لا حصر له من الصفوف أو الأعمدة أو كليهما.
• المَصفوفة الفارغة: هي مصفوفةٌ بدون صفوف ولا أعمدة وتستخدم في برامج الكمبيوتر .
• منقول مصفوفة: هو المَصفوفة الناتجة عن تبديل الأعمدة بالأسطر ويرمز لها A^T  ومن خواصها أن منقول مجموع  مصفوفتين هو مجموع منقول مصفوفتين أي (A+B)^T = A^T+B^T  ، وأيضًا منقول حاصل ضرب مصفوفتين هو حاصل ضرب المصفوفتين بشكلٍ معاكسٍ لمنقولهما أي ( A.B)^T = B^T*A^T
• معكوس مصفوفة: هو المعكوس الضربي للمصفوفة بحيث يكون حاصل ضرب المصفوفة في معكوسها يساوي مصفوفة الواحد أي B = I_n وتدعى المصفوفة B  مقلوب A  ورمزها  A^-1  .

العمليات على المصفوفات

تُجرى عمليتي الجمع والطرح على مصفوفتين بشرط أن يكون لهما نفس الرتبة، أي لهما نفس عدد الصفوف ونفس عدد الأعمدة وتتم العمليتان عنصرًا مع العنصر المقابل له.

لا يُمكن إجراء عملية ضرب بين مصفوفتين إلا إذا تطابق عدد أعمدة المصفوفة الأولى مع عدد صفوف المصفوفة الثانية، بغض النظر عن حجم أو أبعاد المصفوفتين. عند ضرب مصفوفة تحتوي على عنصر واحد فقط في مصفوفة أخرى ذات عناصر متعددة، يتم ضرب هذا العنصر المنفرد بكل عنصر من عناصر المصفوفة الأخرى، وتكون النتيجة مصفوفة بنفس عدد عناصر المصفوفة الأصلية.

في حالة ضرب مصفوفة تتكون من صف واحد فقط في مصفوفة تتكون من عمود واحد فقط، تكون النتيجة مصفوفة تحتوي على عنصر واحد فقط. لعملية ضرب المصفوفات سمات وخواص متعددة، لكنها ليست عملية إبدالية، بمعنى أن حاصل ضرب المصفوفة A في المصفوفة B (A.B) لا يُساوي بالضرورة حاصل ضرب المصفوفة B في المصفوفة A (B.A).

أهمية المصفوفة

تُعدّ المصفوفات وتطبيقاتها أدوات أساسية في مُختلف المجالات العلمية. ففي الفيزياء، تُستخدم في فروعٍ عديدة كالميكانيكا والبصريات الهندسية والكهرومغناطيسية وميكانيكا الكم، لدراسة ظواهر فيزيائية متنوعة كحركة الأجسام الصلبة. كما أنّ لها دورًا هامًا في رسومات الكمبيوتر ومعالجة وعرض النماذج ثلاثية الأبعاد على شاشات ثنائية الأبعاد. بالإضافة إلى ذلك، تُستخدم المصفوفات في نظريات الاحتمالات والإحصاء، وفي المجال الاقتصادي لوصف أنظمة العلاقات الاقتصادية.